Add One Row to Tree

Edit PagePage History

Problem Highlights

• 🔗 Leetcode Link: Add One Row to Tree
• 💡 Problem Difficulty: Medium
• ⏰ Time to complete: 30 mins
• 🛠️ Topics: Binary Trees, Depth First Search, Breath First Search
• 🗒️ Similar Questions: Maximum Depth of Binary Tree, Minimum Depth of Binary Tree

1: U-nderstand

Understand what the interviewer is asking for by using test cases and questions about the problem.

• Established a set (2-3) of test cases to verify their own solution later.
• Established a set (1-2) of edge cases to verify their solution handles complexities.
• Have fully understood the problem and have no clarifying questions.
• Have you verified any Time/Space Constraints for this problem?

• What is the type of tree we are working with?
  • The input tree will be a binary tree
• Can I assume the tree will be complete?
  • No. A node may have less than 2 children
• Can I expect to receive an empty tree as input?
  • No, the input tree can have 1-10000 nodes.
• Is it possible that the depth given is deeper than the given tree?
  • No, the depth given will be within the given tree.
• What is the time and space constraints for this problem?
  • Time O(n) and space O(N)

HAPPY CASE
Input: root = [4,2,6,3,1,5], val = 1, depth = 2
Output: [4,1,1,2,null,null,6,3,1,5]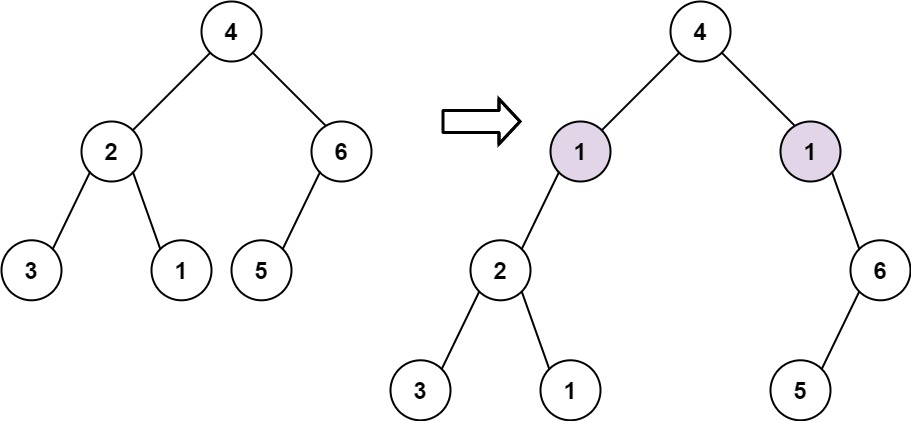

Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]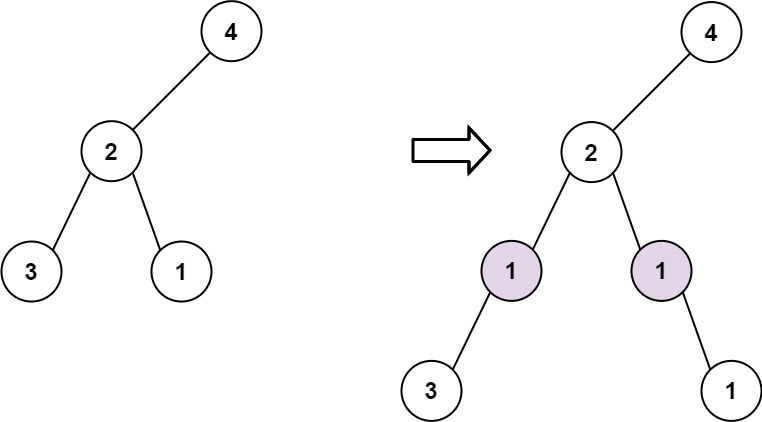

EDGE CASE
Input: root = [1], val=1, depth=1
Output: [1,1,null]

2: M-atch

Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.

If you are dealing with Binary Trees some common techniques you can employ to help you solve the problem:

• Think about appropriate Tree Traversal: Pre-Order, In-Order, Post-Order, Level-Order
  • Since we need to get the height of the tree, we will need to traverse all nodes down the tree, we should recursively go down the tree until we reach the desired depth and insert the node.
• Store nodes within a HashMap to refer to later
  • We don't need to access the nodes or their values after they have been processed, so this technique is not useful for this problem
• Using Binary Search to find an element
  • We are not looking to find an element in this problem so this technique is not useful for this problem
• Applying a level-order traversal with a queue
  • Since we need to find the height of the tree to insert node, we could get nodes by level. a level-order traversal using a queue would be appropriate.

3: P-lan

Plan the solution with appropriate visualizations and pseudocode.

Approach #1 DFS:

General Idea: Recursively decrement the height until the desired depth and add the new node and attach the previous node to left or right branch as appropriate.

1. Handle edgecase root is none
2. Handle edgecase depth is 1: 
3. Handle edgecase depth is 2: Add new node and attach root.left or root.right 
4. Continue to reduce depth and recursively call
4. Return the root

Approach #2 BFS:

General Idea: Level order traversal and decrement the height until the desired depth and add the new node and attach the previous node to left or right branch as appropriate.

1. Handle edgecase depth is 1: Add new node and attach root.
2. Create queue and iterate until desired depth
3. Attach new node to all items in queue
4. Return the root

⚠️ Common Mistakes

• Choosing the wrong traversal type
  • Try to walk through the problem by hand and see the order in which you are processing the nodes. This will clue you into the type of traversal necessary

4: I-mplement

Implement the code to solve the algorithm.

Approach #1 DFS:

class Solution:
  def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:
    # Handle edgecase root is none
    if not root:
      return None
    # Handle edgecase depth is 1: Add new node and attach root.
    elif depth == 1:
      return TreeNode(val, root)
    # Handle edgecase depth is 2: Add new node and attach root.left or root.right
    elif depth == 2:
      root.left = TreeNode(val, root.left, None)
      root.right = TreeNode(val, None, root.right)
    # Continue to reduce depth and recursively call
    else:
      self.addOneRow(root.left, val, depth-1)
      self.addOneRow(root.right, val, depth-1)
    # Return root
    return root

class Solution {
    public TreeNode addOneRow(TreeNode root, int v, int d) {
      // Handle edgecase root is none
      if(root == null) return null;
      // Handle edgecase depth is 1: Add new node and attach root.
      if(d == 1) return new TreeNode(v, root, null);
      // Handle edgecase depth is 2: Add new node and attach root.left or root.right
      if(d == 2){
          root.left = new TreeNode(v, root.left, null);
          root.right = new TreeNode(v, null, root.right);
      // Continue to reduce depth and recursively call
      } else{
          addOneRow(root.left, v, d-1);
          addOneRow(root.right, v, d-1);
      }
      // Return root
      return root;
    }
}

Approach #2 BFS:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:
        # Handle edgecase depth is 1: Add new node and attach root.
        if depth == 1:
            return TreeNode(val, root)

        # Create queue and iterate until desired depth
        queue = [root]
        while depth > 2:
            for _ in range(len(queue)):
                node = queue.pop(0)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            depth -= 1
        
        # Attach new node to all items in queue
        while queue:
            node = queue.pop(0)
            node.left = TreeNode(val, left = node.left)
            node.right = TreeNode(val, right = node.right)
        
        # Return the root
        return root

class Solution {
  public TreeNode addOneRow(TreeNode root, int val, int depth) {
    // Handle edgecase depth is 1: Add new node and attach root.
		if (depth == 1) {
			return new TreeNode(val,root,null);
		}
    
    // Create queue and iterate until desired depth
    Queue<TreeNode> q = new LinkedList<>();
    q.add(root);
    int currDepth = 2;
    while(currDepth++ < depth) {
        int width = q.size();
        while(width-- > 0) {
            TreeNode curr = q.poll();
            if(curr.left != null)
                q.add(curr.left);
            if(curr.right != null)
                q.add(curr.right);
        }
    }
    // Attach new node to all items in queue
    for(TreeNode node : q) {
        node.left = new TreeNode(val,node.left,null);
        node.right = new TreeNode(val,null,node.right);
    }
    // Return the root
    return root;
  }
}

5: R-eview

Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.

• Trace through your code with an input to check for the expected output
• Catch possible edge cases and off-by-one errors

6: E-valuate

Evaluate the performance of your algorithm and state any strong/weak or future potential work.

Assume N represents the number of nodes in binary tree

Approach #1 DFS & #2 BFS Share the same time and space complexity:

• Time Complexity: O(N) because we may need to visit each node in the binary tree
• Space Complexity: O(N) because we used BFS requires O(N/2 + 1). The maximum number of leaf nodes in a perfect binary tree is N/2 and the given the previous node already in the queue. As for DFS we need O(N) to account for unbalanced tree (space is used for the recursion stack). In the general case O(logN) for balanced tree.