Understand what the interviewer is asking for by using test cases and questions about the problem.
- Established a set (2-3) of test cases to verify their own solution later.
- Established a set (1-2) of edge cases to verify their solution handles complexities.
- Have fully understood the problem and have no clarifying questions.
- Have you verified any Time/Space Constraints for this problem?
O(N) Time and O(N) Space.HAPPY CASE
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.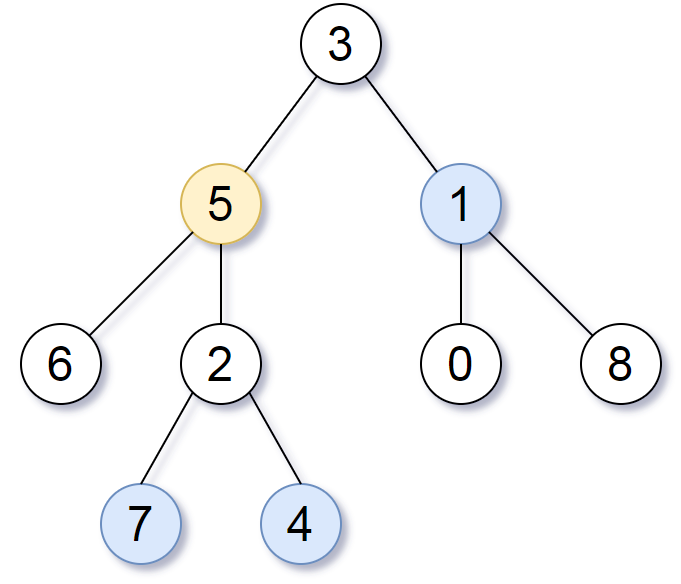
Input: root = [1,2,3], target = 1, k = 1
Output: [2,3]
EDGE CASE
Input: root = [1], target = 1, k = 3
Output: []Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.
If you are dealing with Binary Trees some common techniques you can employ to help you solve the problem:
Plan the solution with appropriate visualizations and pseudocode.
General Idea: Let build a parent map for each node. Then we will recursively traverse from the target node to k nodes away and store those nodes in results
1. Create a helper function to store parentNode in hashmap
a. Basecase: If node is None, return
b. Set current node as key and parent as value
c. Recursively call left child and right child.
2. Create a second helper function to traverse from target node to parent and child nodes and find nodes k away.
a. Basecase: If node is None, or have been traversed, or node is more than k away, return
b. Add node to traversed set, so we do not travel down the same path
c. Upon meeting a node k away from target, add to results
d. Otherwise continue searching, left child, right child, and parent
3. Create Parent Map, traversed set, and results to retain memory.
4. Call getParent function to populate ParentMap
5. Call getNodes function to populate results
6. Return Results⚠️ Common Mistakes
Implement the code to solve the algorithm.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# Create a helper function to store parentNode in hashmap
def populateParentMap(node, parent):
# Basecase: If node is None, return
if node is None:
return
# Set current node as key and parent as value
parentMap[node] = parent
# Recursively call left child and right child
populateParentMap(node.left, node)
populateParentMap(node.right, node)
# DFS function that gets the nodes at a distance k from the target
def getNodes(node, numOfNodesAway):
# Basecase: If node is None, or have been traversed, or node is more than k away, return
if not node or node in traversed or numOfNodesAway > k:
return
# Add node to traversed set, so we do not travel down the same path
traversed.add(node)
# Upon meeting a node k away from target, add to results
if numOfNodesAway == k:
results.append(node.val) # append to result when cnt/distance is k
return
# Otherwise continue searching, left child, right child, and parent
getNodes(node.left, numOfNodesAway + 1)
getNodes(node.right, numOfNodesAway + 1)
getNodes(parentMap[node], numOfNodesAway + 1)
# Create Parent Map, traversed set, and results to retain memory.
parentMap = {}
traversed = set()
results = []
# Call getParent function to populate ParentMap
populateParentMap(root, None)
# Call getNodes function to populate results
getNodes(target, 0)
# Return Results
return resultsclass Solution {
// Create Parent Map, traversed set, and results to retain memory.
List<Integer> answer = new ArrayList<>();
Map<TreeNode, TreeNode> childParentMap = new HashMap<>();
Set<TreeNode> visited = new HashSet<>();
public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
// Call getParent function to populate ParentMap
getParent(root);
// Call getNodes function to populate results
getNodes(target, k);
// Return Results
return answer;
}
// Create a helper function to store parentNode in hashmap
private void getParent(TreeNode node) {
// Basecase: If node is None, return
if(node == null) {
return;
}
// Set current node as key and parent as value
// Recursively call left child and right child
if(node.left != null) {
childParentMap.put(node.left, node);
getParent(node.left);
}
if(node.right != null) {
childParentMap.put(node.right, node);
getParent(node.right);
}
}
// DFS function that gets the nodes at a distance k from the target
private void getNodes(TreeNode node, int k) {
// Basecase: If node is None, or have been traversed, or node is more than k away, return
if(node == null || visited.contains(node)) {
return;
}
// Add node to traversed set, so we do not travel down the same path
visited.add(node);
// Upon meeting a node k away from target, add to results
if(k == 0) {
answer.add(node.val);
return;
}
// Otherwise continue searching, left child, right child, and parent
getNodes(node.left, k-1);
getNodes(node.right, k-1);
getNodes(childParentMap.get(node), k-1);
}
}Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.
Evaluate the performance of your algorithm and state any strong/weak or future potential work.
Assume N represents the number nodes in tree
O(N) because we only need to visit each node in binary tree twice. One time to build the parent map and the second to find nodes k away from target.O(N), by using a hashmap to hold the parent nodes.