Binary Tree Inorder Traversal

Edit PagePage History

Problem Highlights

• 🔗 Leetcode Link: Binary Tree Inorder Traversal
• 💡 Problem Difficulty: Easy
• ⏰ Time to complete: 15 mins
• 🛠️ Topics: Binary Trees, Depth First Search
• 🗒️ Similar Questions: Maximum Depth of Binary Tree, Diameter of Binary Tree, Balanced Binary Tree

1: U-nderstand

Understand what the interviewer is asking for by using test cases and questions about the problem.

• Established a set (2-3) of test cases to verify their own solution later.
• Established a set (1-2) of edge cases to verify their solution handles complexities.
• Have fully understood the problem and have no clarifying questions.
• Have you verified any Time/Space Constraints for this problem?

• Can I expect to receive an empty Tree as input?
  • Yes, there may be an empty Tree as input
• What is the time and space constraints for this problem?
  • O(n) time complexity and O(n) space complexity

HAPPY CASE
Input: root = [1,null,2,3]
Output: [1,3,2]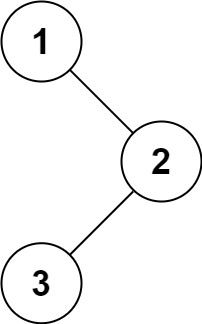

Input: root = [1]
Output: [1]

EDGE CASE
Input: root = []
Output: []

2: M-atch

Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.

If you are dealing with Binary Trees some common techniques you can employ to help you solve the problem:

• Think about appropriate Tree Traversal: Pre-Order, In-Order, Post-Order, Level-Order
  • Since are traversing a binary tree. We should think about the order, and the order given is In-Order.
• Store nodes within a HashMap to refer to later
  • We don't need to access the nodes or their values after they have been processed, so this technique is not useful for this problem
• Using Binary Search to find an element
  • We are not looking to find an element in this problem so this technique is not useful for this problem
• Applying a level-order traversal with a queue
  • Since are traversing tree with the idea of returning In-Order values. Level Order Tree Traversal does not apply very well here.

3: P-lan

Plan the solution with appropriate visualizations and pseudocode.

General Idea: In-Order traverse is left-process-right. Lets go left, store, and go right for each node.

1. Create a helper function to recursively progress through the nodes.
    a. Basecase, root is none. 
    b. Go to left node
    c. Store node value into results
    d. Go to right node
2. Create results array
3. Call helper function to build results
4. Return results 

⚠️ Common Mistakes

• Choosing the wrong traversal type
  • Try to walk through the problem by hand and see the order in which you are processing the nodes. This will clue you into the type of traversal necessary
  • Suppose you choose pre order traversal, we would go check - left - right . Will not produce the correct order of nodes
  • Suppose you choose post order traversal, we would go left - right - check. Will not produce the correct order of nodes
• Failing to recognize the need for a helper function to store results during recursive processing of nodes. ## 4: I-mplement

Implement the code to solve the algorithm.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # Create a helper function to recursively progress through the nodes
        def helper(root: Optional[TreeNode]):
            # Basecase, root is none. 
            if not root:
                return

            # Go to left node
            helper(root.left)

            # Store node value into results
            results.append(root.val)

            # Go to right node
            helper(root.right)
        
        # Create results array
        results = []

        # Call helper function to build results
        helper(root)

        # Return results 
        return results

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        // Create results array
        List<Integer> ret = new ArrayList<>();
        // Call helper function to build results
        dfs(root, ret);
        // Return results 
        return ret;
    }

    // Create a helper function to recursively progress through the nodes
    private void dfs(TreeNode node, List<Integer> ret) {
        // Basecase, root is none. 
        if (node == null) {
            return;
        }
        // Go to left node
        dfs(node.left, ret);
        // Store node value into results
        ret.add(node.val);
        // Go to right node
        dfs(node.right, ret);
   }
}

5: R-eview

Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.

• Trace through your code with an input to check for the expected output
• Catch possible edge cases and off-by-one errors

6: E-valuate

Evaluate the performance of your algorithm and state any strong/weak or future potential work.

Assume N represents the number of nodes in Tree

• Time Complexity: O(N) because we need to visit each node in binary tree.
• Space Complexity: O(N) because we need to create a results array with the values from all the nodes.