Codepath

Crawler Log Folder
Edit PagePage History

Problem Highlights

1: U-nderstand

Understand what the interviewer is asking for by using test cases and questions about the problem.

  • Established a set (2-3) of test cases to verify their own solution later.
  • Established a set (1-2) of edge cases to verify their solution handles complexities.
  • Have fully understood the problem and have no clarifying questions.
  • Have you verified any Time/Space Constraints for this problem?

Be sure that you clarify the input and output parameters of the problem:

  • How should I handle an empty log file?
    • All log files will have at least one input
  • What are the time and space constraints?
    • Time should be O(N) and space should be O(1) including the recursive stack, N being the length of the logs

Run through a set of example cases:

HAPPY CASE
Input: logs = ["d1/","d2/","../","d21/","./"]
Output: 2
Explanation: Use this change folder operation "../" 2 times and go back to the main folder.

image1

Input: logs = ["d1/","d2/","./","d3/","../","d31/"]
Output: 3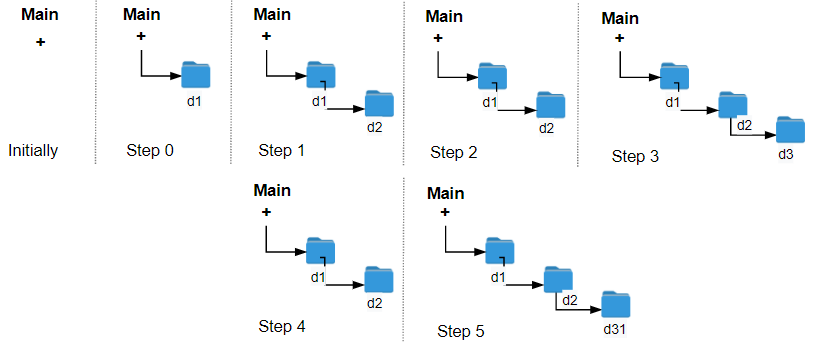

image2

EDGE CASE 
Input: logs = ["../"]
Output: 0

2: M-atch

Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.

  • Sort
    • Not helpful, we need to maintain the relative order of the logs
  • Two pointer solutions (left and right pointer variables)
    • Not helpful, we need to move in one direction
  • Storing the elements of the array in a HashMap or a Set
    • Not helpful, how does the hashmap help us find the distance between characters
  • Traversing the array with a sliding window
    • Not helpful, we are not looking for a window size
  • Stack
    • When dealing with file system traversal, stack is a good choice

3: P-lan

Plan the solution with appropriate visualizations and pseudocode.

General Idea: We will recursively find the depth of the file traversal logs and that will be the minimum operations to return to root.

1. Write a recursive function to drill into the file system.
    a. Set the basecase: Out of bound.
    b. Update depth base on log function string
    c. Call recursive function on next log item
2. Call the recursive function 
3. Return the result.

General Idea: We will iteratively find the depth of the file traversal logs and that will be the minimum operations to return to root.

1. Create a stack
2. Add/Remove items from stack 
3. Return the size of stack.

⚠️ Common Mistakes

  • Using iterative approach will work here, however the interviewer wants the recursive solution.

4: I-mplement

Implement the code to solve the algorithm.

Recursive

class Solution:
    def minOperations(self, logs: List[str]) -> int:
      depth = 0
      # Write a recursive function to drill into the file system
      def helper(i):
        # Set the basecase: Out of bound
        if i > len(logs) - 1:
          return 

        # Update depth base on log function string
        nonlocal depth
        if logs[i] == "../":
          if depth > 0:
            depth -= 1
        elif logs[i] == "./":
          pass
        else:
          depth  += 1
        
        # Call recursive function on next log item
        helper(i + 1)

      # Call the recursive function 
      helper(0)

      # Return the result
      return depth
class Solution {
  int depth = 0;
  public int minOperations(String[] logs) {
    // Call the recursive function 
    helper(logs, 0);
    // Return the result
    return depth;
  }
  // Write a recursive function to drill into the file system
  private void helper(String[] logs, int i) {
    // Set the basecase: Out of bound
    if (i > logs.length - 1) return;

    // Update depth base on log function string
    if (logs[i].equals("../")) {
      if (depth > 0) {
        depth--;
      }
    } else if (logs[i].equals("./")) {
      ;
    } else {
      depth++;
    }

    // Call recursive function on next log item
    helper(logs, i+1);
  }
}

Iterative

class Solution:
  def minOperations(self, logs: List[str]) -> int:
    # Create a stack
    stack = []

    # Add/Remove items from stack
    for log in logs:
      if log == "../":
        if stack:
          stack.pop()
      elif log == "./":
        continue
      else:
        stack.append(log)
    
    # Return the size of stack
    return len(stack)
class Solution {
  public int minOperations(String[] logs) {
    // Create a stack
    var stack = new Stack<String>();
    //Add/Remove items from stack
    for(var log : logs){
      if(log.equals("../")){
          if(!stack.empty())
              stack.pop();
      }else if(log.equals("./")){

      }else{
          stack.push(log);
      }
    }
    // Return the size of stack.
    return stack.size();
  }
}

5: R-eview

Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.

  • Trace through your code with an input to check for the expected output
  • Catch possible edge cases and off-by-one errors

6: E-valuate

Evaluate the performance of your algorithm and state any strong/weak or future potential work.

Assume N represents the size of array

  • Time Complexity: O(N) because we will run the algorithm once to process all logged commands
  • Space Complexity: O(1) because the recusive call does not need to be stored in memory. Technically this called Tail recursion, a recursion of a function where it does not consumes stack space and hence prevents stack overflow.
Fork me on GitHub